При нахождении силы будет использован закон сохранения энергии и принцип возможных перемещений.
Определим силу 
, приложенную к 
-му механическому узлу ( -м механическим зажимам).
Предполагается, что возможное перемещение 
-го механического узла, происходит за время 
; при этом все другие механические координаты остаются неизменными, то есть 
при 
.
Закон сохранения энергии должен сохраняться в течение всего возможного перемещения.
Различные энергии, соответствующие возможному перемещению:
энергия, поступающая на все 
электрических зажимов
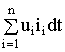, (1.105)
где 
;
энергия, поступающая на -е “механические зажимы”
; (1.106)
изменение запасенной магнитной энергии поля связи
; (1.107)
энергия рассеяния 
.
Закон сохранения энергии: сумма подводимой энергии равняется изменению запасенной энергии. То есть, из (1.105)-(1.107):
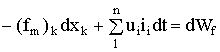. (1.108a )
И, следовательно,
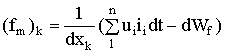. (1.108b )
Или
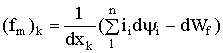. (1.109)
После того, как определены независимые электрические и независимые механические координаты, уравнение (1.109) дает силу, приложенную к k-му узлу, и скорость k-го механического узла 
. Таким образом, определяются механические характеристики (сила - скорость) на механических зажимах электромеханической системы.
По принципу Д’Аламбера сила из уравнений (1.109) должна быть включена в уравнение равновесия для k-го механического узла
, (1.110)
где 
– сила инерции, 
– внешняя механическая сила, 
– сила упругости. Считается, что эти три силы включены в механическую часть системы.
При определении возможно любое произвольное изменение электрических переменных. Но уравнения связи (1.102) и (1.104) должны быть соблюдены.
Для вычисления энергии магнитного поля считаем, что конечные значения 
каждой катушки и конечные положения катушек 
получены любыми произвольными изменениями как электрических, так и механических переменных от нуля до конечных значений.
Определим возможное перемещение для точки, характеризующей состояние системы в семействе кривых намагничивания
. (1.111)
Функции (1.111) устанавливают зависимость 
от 
и 
, которые должны поддерживаться в течение возможного перемещения, определенного уравнением (1.108a ).
Запасенная магнитная энергия 
является силовой функцией и представляется однозначной зависимостью
, (1.112)
Второе слагаемое в правой части (1.109) – полный дифференциал, поэтому
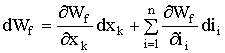. (1.113)
В (1.113) все переменные и – независимые. Это определяет, что 
– производная по 
при постоянстве других токов и перемещений 
, 
– приращение магнитной энергии за счет изменения координаты 
при 
; 
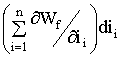– приращение магнитной энергии за счет изменения токов контуров при 
.
Общее выражение для 
из (1.111):
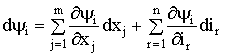. (1.114)
Если при возможном перемещении 
при 
, то
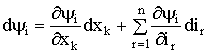. (1.115)
В (1.115) производные 
и 
берутся при условии, что все остальные и постоянны.
Воспользуемся уравнением (1.115) при определении слагаемого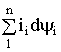 
в уравнении (1.109):
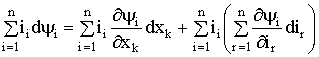. (1.116)
Подставив (1.116) и (1.113) в (1.109), получим:
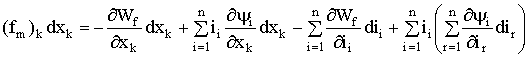. (1.117)
Группируя слагаемые и изменяя индексы в последнем слагаемом уравнения (1.117), получим:
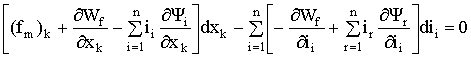. (1.118)
В первых квадратных скобках левой части (1.118) первое слагаемое 
– механическая работа, совершаемая определяемой силой 
при элементарном перемещении 
; приращение энергии поля (второе слагаемое) и энергия 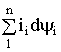, подведенная от источников (третье слагаемое), обусловлены именно перемещением .
Уравнение (1.118) не определяет никаких ограничений на законы изменения и . Выражения в квадратных скобках – функции и , но не зависят от их изменения (уравнения (1.111) и (1.112)). Уравнение (1.118), полученное из законов сохранения энергии, является справедливым всегда, при любых изменениях и . Это справедливо тогда и только тогда, когда выражения в квадратных скобках (множители при 
и 
) тождественно равны нулю.
Поэтому электромагнитная сила определяется уравнением:
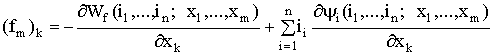. (1.119)