В этом разделе представляется связь движения в электромеханической системе с изменениями магнитного поля. Эти изменения могут быть определены изменением поля во времени при неизменном положении рассматриваемого контура (1) в пространстве (рис.1.24) и изменением магнитного поля в пространстве относительно контура при движении его в поле неизменной индукции ![]() (рис.1.25). Движение магнитного поля можно представить функционалом
(рис.1.25). Движение магнитного поля можно представить функционалом ![]() , который представляет потокосцепление контура зависящим от тока
, который представляет потокосцепление контура зависящим от тока ![]() , обусловливающего поле, и координаты
, обусловливающего поле, и координаты ![]() , определяющей мгновенное положение контура в поле. Ток
, определяющей мгновенное положение контура в поле. Ток ![]() зависит от времени
зависит от времени ![]() (
(![]() ) и координата
) и координата ![]() зависит от времени (
зависит от времени (![]() ). Поэтому для электродвижущей силы (ЭДС), в соответствии с уравнением (1.15):
). Поэтому для электродвижущей силы (ЭДС), в соответствии с уравнением (1.15):
Рис.1.24
Рис.1.25
![]() . (1.44)
. (1.44)
Первое слагаемое в правой части этого уравнения называют ЭДС трансформации ![]() (или ЭДС пульсации); она индуктируется в контуре вследствие изменения тока
(или ЭДС пульсации); она индуктируется в контуре вследствие изменения тока ![]() со скоростью
со скоростью ![]() ; при этом координата
; при этом координата ![]() . Уравнение (1.44) определяет, что трансформаторная ЭДС зависит от параметра
. Уравнение (1.44) определяет, что трансформаторная ЭДС зависит от параметра
![]() - (1.45)
- (1.45)
динамической (или дифференциальной) индуктивности.
Второе слагаемое в правой части уравнения (1.44) – ЭДС движения или ЭДС вращения ![]() , поскольку движение электрических машин обычно вращательное. ЭДС движения
, поскольку движение электрических машин обычно вращательное. ЭДС движения
![]() - (1.46)
- (1.46)
наводится в контуре при изменении координат ![]() , определяющих изменения положения контура в части пространства, захватываемого изменяющимся потокосцеплением
, определяющих изменения положения контура в части пространства, захватываемого изменяющимся потокосцеплением ![]() . При этом магнитное состояние рассматриваемой части пространства определяется при заданном постоянном значении тока
. При этом магнитное состояние рассматриваемой части пространства определяется при заданном постоянном значении тока ![]() ; поэтому ЭДС движения рассчитывается по изменениям (
; поэтому ЭДС движения рассчитывается по изменениям (![]() ) статической индуктивности (
) статической индуктивности (![]() ), обусловленным изменением координаты
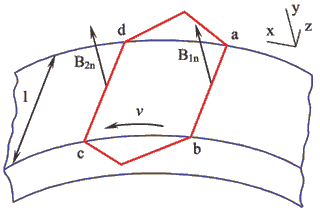
), обусловленным изменением координаты ![]() . Уравнение (1.46) может быть приведено к более удобному виду, поскольку оно должно определяться с учетом конструкции активной зоны электрической машины. Пусть на цилиндрической поверхности магнитопровода (рис.1.26), имеющей длину
. Уравнение (1.46) может быть приведено к более удобному виду, поскольку оно должно определяться с учетом конструкции активной зоны электрической машины. Пусть на цилиндрической поверхности магнитопровода (рис.1.26), имеющей длину ![]() , расположен контур
, расположен контур ![]() с числом витков
с числом витков ![]() ; стороны контура очень узки и совпадают с образующими поверхности. Считается, что нормальная составляющая индукции
; стороны контура очень узки и совпадают с образующими поверхности. Считается, что нормальная составляющая индукции ![]() на всей длине
на всей длине ![]() стороны контура не изменяется; не учитывается, вследствии малости, часть потока, не проходящая через площадку
стороны контура не изменяется; не учитывается, вследствии малости, часть потока, не проходящая через площадку ![]() на цилиндрической поверхности. Стороны контура
на цилиндрической поверхности. Стороны контура ![]() и
и ![]() находятся в точках
находятся в точках ![]() и
и ![]() , соответственно, поверхности якоря и
, соответственно, поверхности якоря и ![]() .
.
Потокосцепление контура
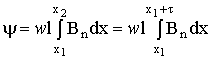 . (1.47)
. (1.47)
Индуктированная ЭДС вращения в соответствии с (1.46),
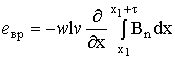 . (1.48)
. (1.48)
На основании теоремы Лейбница-Ньютона интегрального исчисления
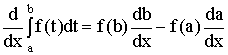 ,
,
а ЭДС вращения
![]() . (1.49)
. (1.49)
Суммарная ЭДС в контуре
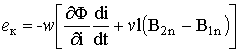 . (1.50)
. (1.50)
|
Значения ЭДС трансформации и ЭДС вращения в суммарной ЭДС |
|
|