Явление электромагнитной индукции установлено Майклом Фарадеем в 1831 году. После многолетней (около 10 лет) серии опытов им был установлен закон, определяющий это явление.
|
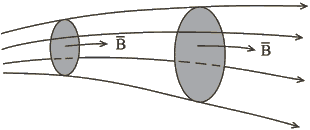
Рассмотрим часть пространства, в котором есть магнитное поле. В этой части есть трубчатая поверхность, образованная совокупностью линий магнитной индукции (рис.1.6). Эта часть пространства – трубка магнитной индукции. Все пространство поля, можно представить в виде совокупности трубок, а каждую трубку изображать одной линией магнитной индукции, совпадающей с осью трубки. Если поток через поперечное сечение трубки магнитной индукции равен единице (1 Вебер), то такую трубку называют единичной; линию магнитной индукции, изображающую единичную трубку, называют единичной линией магнитной индукции. |
|
|
Магнитный поток 
через поверхность 
равен числу 
единичных трубок магнитной индукции (равен числу единичных линий магнитной индукции), охватываемых контуром 
, ограничивающим эту поверхность (рис.1.7). Линии магнитной индукции всюду непрерывны. Поэтому линия магнитной индукции может войти внутрь контура , затем выйти из него, сцепившись с ним, или перерезать его где-либо. Это значит, что изменение 
потока, охваченного контуром , должно равняться числу единичных линий магнитной индукции D n , сцепленных с контуром либо им перерезанных:
. (1.7)
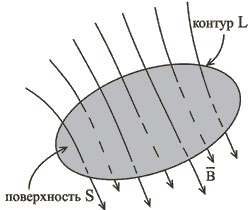
Рис.1.7
Закон электромагнитной индукции (см.1.5) имеет вид:
- (1.8)
электрический заряд, перенесенный за время 
через поперечное сечение цепи индуктированного тока, равен взятому со знаком "минус" отношению числа единичных линий магнитной индукции, сцепленных с контуром L или перерезанных им за это время, к сопротивлению цепи.
М.Фарадей в такой форме и дал закон электромагнитной индукции. То, что , должно быть справедливо для любого изменения потока в течение любого промежутка времени .
Вернемся, однако к уравнению (1.5). Очень важным является то, что поток через поверхность , ограниченную контуром цепи , обусловлен всеми внешними по отношению к рассматриваемой цепи токами и намагниченными телами, а также и током в самой рассматриваемой цепи. Поэтому в (1.5) – приращение результирующего потока через поверхность , ограниченную контуром цепи L . При бесконечно малом изменении потока
. (1.9)
В (1.9) 
– электрический заряд, переносимый через поперечное сечение цепи за промежуток времени 
. За это время поток изменится на 
. Поэтому
, (1.10)
или
. (1.11)
Произведение в левой части 
, согласно закону Кирхгофа, равно электродвижущей силе, действующей в рассматриваемой цепи (пробная рамка - гальванометр). Поэтому в правой части (1.11) – электродвижущая сила электромагнитной индукции:
- (1.12)
электродвижущая сила 
, индуктируемая в цепи при изменении магнитного потока через поверхность , ограниченную контуром цепи, равна скорости (
) изменения потока , взятой со знаком "минус". Эта формулировка закона электромагнитной индукции принадлежит Дж.К.Максвеллу.
Уравнение Максвелла для индуктированной электродвижущей силы по смыслу может быть применено только к замкнутым контурам. Выражение закона электромагнитной индукции (1.8) определяет действием пересечение контура единичными линиями магнитной индукции и может быть применено и к отрезкам контура (отдельным его участкам).