Определения в разделах 1.14-1.17 электромагнитной силы, действующей в электромеханической системе, обусловлены проявлениями движения. Эти проявления движения – изменения координат  , токов   и потокосцеплений  .

В указанных разделах уравнения движения электромеханических систем были получены из закона сохранения энергии и принципа возможных перемещений в предположении бесконечно малых изменений в системе.

При анализе систем развит и другой подход к описанию их динамики, основанный на принципах "больших" движений в системах.

Конкретная физическая система имеет единственную динамическую траекторию  поведения, независимо от способа получения уравнений движения.

Известно, что наиболее фундаментальным принципом "больших" движений в системах является принцип Гамильтона.

Принцип Гамильтона формулируется в терминах вариационного исчисления. Мы не будем сосредоточивать внимание на вопросах математики, а скажем, что из принципа Гамильтона для энергетической функции  , зависящей от   переменных (  координат  и   скоростей  ) следует уравнение Эйлера-Лагранжа:

 

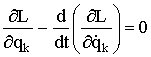         при  .                   (1.143)

 

Координаты   и скорости   называются соответственно обобщенными координатами и скоростями

Здесь для описания движения системы выбрана силовая функция Лагранжа, или лагранжиан,  .

Уравнение (1.143) определяет динамическую траекторию системы, как только найдена функция Лагранжа для этой системы. Оно особенно полезно при изучении электромеханических систем, поскольку дает полные уравнения движения. При этом использование принципа Д'Аламбера и законов Кирхгофа не является необходимым.

          В классической механике впервые лагранжиан определен как разность между кинетической энергией   и потенциальной энергией  , то есть . Это определение не распространялось на нелинейные системы.

Можно разложить   на две функции, которые будут справедливы и для нелинейных случаев.

Если лагранжиан  , то дифференциал от 

 

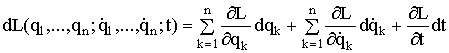    .            (1.144)

 

Поскольку   по определению – силовая функция, то для нахождения ее можно выбрать путь интегрирования так, что при интегрировании по   все   остаются постоянными, а при интегрировании по   постоянны все  . Кроме того, интегрирование можно выполнять для определенного значения времени  :

 

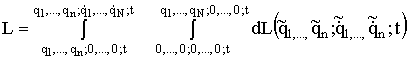  .            (1.145)

 

Подставляя в (1.145)   из уравнения (1.144), получаем при указанных изменениях переменных:

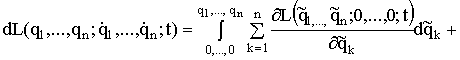
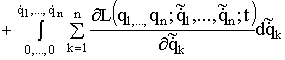  .                            (1.146)

 

Первая из функций в правой части (1.146) зависит от   и   и совершенно не зависит от скоростей системы  . Она точно равна потенциальной энергии, взятой со знаком минус. Поэтому обобщенная сила

 

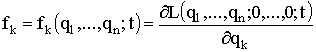  ,                      (1.147)

 

а потенциальная энергия   определяется как

 

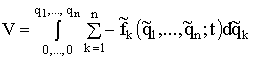                                     (1.148)

(сравните с уравнением (1.106)).

Второе слагаемое в правой части (1.146) является функцией конечных значений координат   и скоростей  . В линейном случае оно по форме точно соответствует кинетической энергии в механике или запасенной энергии для системы катушек индуктивностей, если  .

В нелинейном случае для электромеханических систем уравнение вида

 

                                                

 

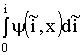
определяет магнитную коэнергию.

Поэтому, определяя обобщенный импульс как

 

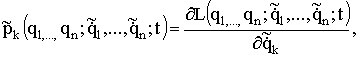                (1.149)

 

для коэнергии   получим:

 

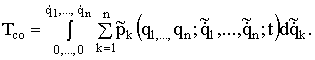                         (1.150)

 

В соответствии с (1.148) и (1.150) лагранжиан принимает вид:

 

  .      (1.151)

 

Такое определение лагранжиана особенно ценно, поскольку оно используется при решении нелинейных задач, и в том числе – задач электромеханики.

В уравнении Лагранжа (1.143) определяют 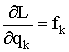  как потенциальную силу, а  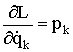 как импульс кинетических потенциалов.

Необходимо установить, какие переменные как электрических, так и механических систем нужно выбрать в качестве обобщенных переменных  ,  ,   и  . Для механической части системы здесь определена ясность в связи с укоренившимися соответствиями. Пусть механическая система состоит из материальных тел и пружин. Тогда обобщенные переменные системы:

  – обобщенные механические координаты (механические перемещения) –  ;

  – обобщенные механические скорости (механические скорости) –  ;

  – обобщенные механические силы (механические силы, зависящие только от положения)   ;

  – обобщенные механические импульсы (механические импульсы, обычно зависящие только от скорости, но могущие зависеть от координат и скоростей) 

В общем случае электромеханический преобразователь  запасает в поле как электрическую  , так и магнитную энергию  . Как соотнести их с понятиями потенциальной и кинетической энергии? Возможны два вида соотношений. Остановимся на одном из них:   – отождествлена с потенциальной энергией, а   – c кинетической энергией. Здесь нельзя    отождествлять с энергией, поступившей в систему из электрических цепей.

В этом случае для электромагнитной части системы:

  – обобщенные электрические координаты (электрические заряды  );

  – обобщенные электрические скорости (электрические токи );

  – обобщенные электрические силы (электрические напряжения с обратным знаком –  );

  – обобщенные электрические импульсы (магнитные потокосцепления –  )

Представленное выше уравнение Лагранжа (1.143) определяет консервативные системы. Неконсервативные силы связей исключаются правильным выбором обобщенных координат. Для систем, у которых неконсервативные силы связей не зависят от обобщенных координат и скоростей, а являются постоянными или зависят только от времени, можно определить неконсервативный лагранжиан.

Уравнение Эйлера-Лагранжа (1.143) содержит два слагаемых – две обобщенные силы. Эти слагаемые определяют, что при динамическом равновесии консервативной системы сумма всех сил, действующих по  -й координате, равна нулю.

Если рассматривается действие неконсервативной силы   по  -й координате   совместно с консервативными силами системы, то согласно принципу Д'Аламбера сумма всех сил включая неконсервативные, при динамическом равновесии, равна нулю. Тогда уравнение Эйлера-Лагранжа, распространенное на неконсервативную систему:

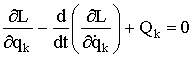 .                            (1.152)

 

Примерами неконсервативных сил   в электромеханической системе могут служить напряжение, приложенное к зажимам электрической схемы, момент на валу генератора.

При составлении лагранжиана необходимо учесть рассеяние в системе. Для этого в уравнение Эйлера-Лагранжа вводят функцию  , зависящую от скорости, и называют ее функцией потерь и определяют как

 

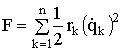 .                                          (1.153)

 

Функция   имеет размерность мощности и определяет в уравнении Лагранжа неконсервативную диссипативную силу 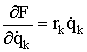 . Это отрицательная сила, приложенная к системе. Учет в уравнении Эйлера-Лагранжа (1.152) для неконсервативной части системы диссипативных составляющих по (1.153) дает уравнение динамического равновесия:

 

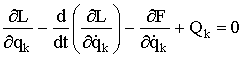 .                           (1.154)

 

Может быть определен порядок получения уравнений движения для любой системы при использовании консервативного лагранжиана и суммирования сил:

1.   Определяют систему обобщенных переменных   неконсервативные силы , появляющиеся за счет источников энергии, и силы  , которые возникают за счет потерь.

2.   Используя определенные обобщенные переменные, записывают выражения для кинетической коэнергии   и потенциальной энергии   для консервативной части системы по (1.150) и (1.148);

3.   Определяют неконсервативные силы, связанные с рассеянием, и записывают функцию рассеяния  ;

4.   Находят консервативный лагранжиан  ;

5.   Подставляют   в уравнение Лагранжа

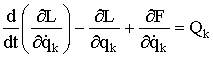
и, проводя дифференцирование при изменении   от 1 до  , получают   динамических уравнений системы.