Дуальность означает двойственность, а аналогия – соответствие.

Системы, для которых различные физические процессы представляются одной и той же системой интегро-дифференциальных уравнений, называются аналоговыми.

Формальное решение дифференциальных уравнений для какой-либо физической системы является формальным решением аналогичной задачи.

Инженер-электромеханик, знакомый с аналитическими методами исследования переходных (преобразование Лапласа) и установившихся (комплексный метод) процессов, имеет возможность анализировать механические, тепловые или акустические системы, представленные аналогичной электрической схемой замещения.

В теории электрических цепей существует принцип дуальности. В соответствии с этим принципом имеется возможность найти электрическую схему, уравнения равновесия которой, полученные из уравнений для контуров для напряжений, имеют ту же математическую запись, что и уравнения равновесия другой электрической схемы, записанные на основе уравнений для узлов для токов. Две дуальные электрические схемы являются аналогами. Термин "аналог" обычно используют при сравнении различных физических систем, а термин "дуальность" – для электрических схем, которые имеют математически подобные уравнения.

Смысл дуальности можно объяснить, если поменять независимые и зависимые переменные в уравнениях, описывающих поведение элементов схемы.

Рассмотрим уравнения связи между напряжениями и токами для трех основных параметров электрической цепи: сопротивления, индуктивности и емкости (дуальные пары).

 

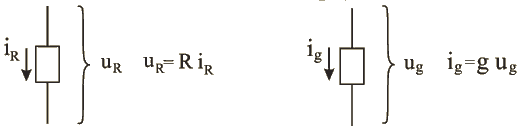
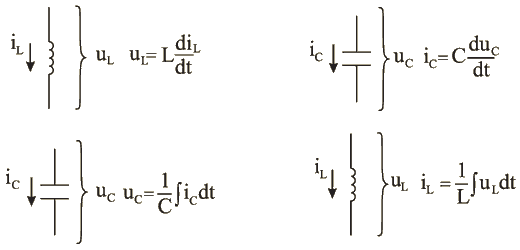
Дуальность не подразумевает эквивалентность; дуальность означает, что математические представления цепей аналогичны.

В электромеханике часто используют эквивалентные схемы преобразователей. Эквивалентные схемы всегда возможны и часто применяются для упрощения решения задачи. Эквивалентные схемы могут быть двух типов:

- схемы, которые производят одинаковый эффект на заданных зажимах;

- схемы, которые имеют идентичные с заданной схемой уравнения.

Обычно схемы замещения (эквивалентные схемы) используются с целью облегчить вычисления, анализ или проектирование.

Рассмотрение общих вопросов дуальности и аналогий для электромеханических преобразователей удобно сделать на конкретных примерах.

На рис.1.45 представлена параллельная механическая цепь.

 

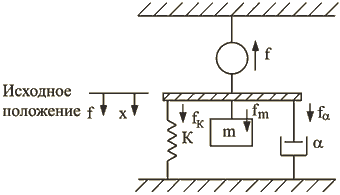
Рис. 1.45.

 

Она содержит массу  , связанную с пружиной  : на них действуют сила трения  и внешняя сила  .

Дифференциальное уравнение, которому подчиняется движение системы, получим, используя принцип Д'Аламбера. Уравнение сил

                                           (1.137)

 

можно записать в виде:

 

 .                              (1.138)

где   - перемещение от положения свободного равновесия; v - скорость движения системы.

Последнее уравнение математически идентично уравнению равновесия для схемы рис. 1.46:

 

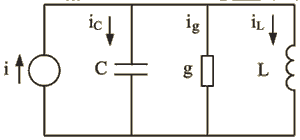
Рис. 1.46.

 

 .                                          (1.139)

Дифференциальные уравнения (1.138) и (1.139) и их решения имеют одну и ту же форму; поэтому схемы (1.45) и (1.46) можно выбрать в качестве аналогов.

Рассмотрим последовательную механическую цепь (рис. 1.47):

 

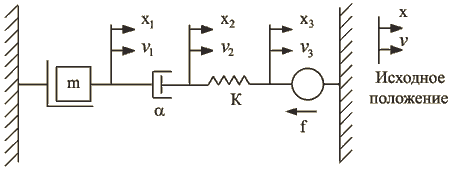
Рис. 1.47

 

Поскольку  , то равновесие этой системы может быть определено как

 

                                                  (1.140)

или

  .                              (1.141)

 

Рассмотрим последовательную цепь R, L, C (рис. 1.48):

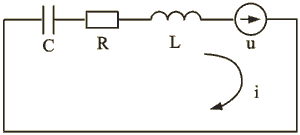
Рис. 1.48.

 

Дифференциальное уравнение этой цепи

 

 .                                           (1.142)

 

Сравнение уравнений (1.141) и (1.142) убеждает в том, что они аналогичны по форме. Последовательные механическая и электрическая цепи – прямые аналоги друг друга.

Параллельная и последовательная электрические цепи электрически дуальны; параллельная и последовательная механические цепи механически дуальны.

Рассмотренные выше примеры определяют прямые аналогии.

Однако, вследствие природы параллельной и последовательной электрической и механической цепей можно найти связь, например, между параллельной механической и последовательной электрической цепями, и наоборот. Такая связь определяет обратные аналогии.