Одним из основных принципов механики, дающим общий метод решения задач динамики и статики является принцип Д'Аламбера‑Лагранжа. Он объединяет принцип Д'Аламбера и принцип возможных перемещений.

Фундаментальное соотношение сил в статике заключается в том, что при равновесии сумма всех сил, действующих на тело, равна нулю. Это заключение использовал Д'Аламбер, сформулировав положение: при динамическом равновесии механических систем сумма всех сил равна нулю. При этом полагается, что к заданным (активным) силам, действующим на точки механической системы, и реакциям связей присоединяются силы инерции. Для многоконтурной механической системы в соответствии с принципом Д'Аламбера для  -го механического узла

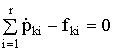 ,                                            (1.133)

где   – i-я инерционная сила k-го узла;  –  ‑я механическая сила, включая любые силы связи, приложенная к  -му узлу.

Предполагается, что каждый механический узел представляется только одной координатой   и имеет только одну степень свободы.

          Чтобы удовлетворить принципу Д'Аламбера, необходимо принять равной нулю сумму всех перемещений или скоростей вдоль любого  -го механического контура:

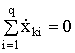 ,                                                   (1.134)

где   –  -я скорость  ‑го контура.

Уравнения (1.133) и (1.134) определяют принцип суммирования сил и принцип возможных перемещений (принцип суммирования скоростей).

Для электрических цепей подобные динамические уравнения равновесия установлены Кирхгофом:

сумма всех падений напряжения вдоль  -го контура равна нулю (принцип суммирования сил) -

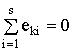 ,                                                    (1.135)

где   – -е напряжение в  -м контуре;

сумма всех токов в k-м узле должна равняться нулю (принцип суммирования скоростей) -

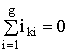 .                                                    (1.136)

Уравнения (1.133-1.136) полностью и связанно определяют движение электромеханических систем: электромагнитные силы подчиняются принципу Д'Аламбера (1.133), а в уравнениях Кирхгофа (1.135) и (1.136) составляющие, содержащие производные по времени  , проявляют эффект механического движения.