Энергетическое состояние электромеханической системы определяют:

энергия, поступающая из внешних цепей – уравнение (1.105.);

изменение энергии, запасенной в магнитном поле – уравнение (1.107);

механическая энергия – уравнение (1.106).

Изменения состояния по этим уравнениям определены изменениями  ,   и  . При этих изменениях энергетические функции состояния системы:

запасенная магнитная энергия

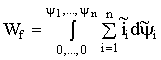 .                                            (1.103a)

и коэнергия

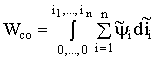 .                                             (1.120a)

При известной связи между энергией и коэнергией

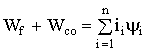  ,                                    (1.121)

значения запасенной энергии   и коэнергии  , а, следовательно, и значение электромагнитной силы   можно определить при любом задании независимых переменных:

  .                                 (1.102)

или

  .                                   (1.104)

Пусть независимые переменные   и  . Тогда уравнения электромагнитной силы (в сокращенной записи):

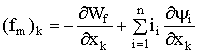 .                                              (1.119)

и

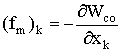 .                                                    (1.122)

Сила   вычисляется в обоих уравнениях при постоянных (неизменных) токах. При этом значения   и   точно соответствуют   и   в уравнении (1.64) и графическим представлениям энергетического процесса на рис.1.31 и 1.33; значение   по уравнению (1.122) соответствует изменению   по уравнению (1.67) и представлению процесса на рис.1.34.

Если независимыми переменными являются потокосцепления   и координаты  , то электромагнитная сила

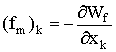 .                                                     (1.127)

или

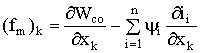 .                                    (1.128)

Изменение (уменьшение) энергии  , запасенной в магнитном поле при неизменном потокосцеплении  , в уравнении (1.127) соответствует совершению механической работы в процессе, представленном ранее на рис.1.32.

Уравнение (1.128) можно получить при подстановке в определенное уравнение электромагнитной силы

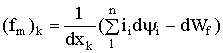                                 (1.109)

значения энергии, запасенной в магнитном поле,

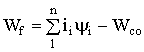
из уравнения (1.121) при условиях (1.102)

Условие постоянства токов   или потокосцеплений   при вычислении электромагнитной силы – математические ограничения, налагаемые посредством выбора независимых переменных и, вообще, не имеют никакого отношения к условиям связей с внешними электрическими цепями.

С другой стороны, эти условия объясняют отдельные случаи электрических связей системы и внешних цепей. Если потокосцепления   приняты постоянными, то равны нулю, и обмен энергией между магнитным полем и источниками электрической энергии отсутствует. Поэтому преобразование энергии происходит в связи между магнитным полем и механической системой; сила здесь определяется по уравнению (1.127) отрицательной скоростью изменения магнитной энергии при механическом перемещении при постоянных потокосцеплениях. Характер и соотношения связей в этом случае совпадают с математическими ограничениями метода.

Будем считать, что система возбуждается от источников тока. Независимые переменные в этом случае – токи и координаты  . Тогда электромагнитная сила  определяется положительной скоростью изменения магнитной коэнергии в процессе механического перемещения по уравнению 1.122). Как и в предыдущем случае, здесь характер и соотношение электрических связей совпадают с математическими ограничениями метода.