Уравнение для вычисления электромагнитной силы, может быть получено через коэнергию  . Она определяется следующим выражением:

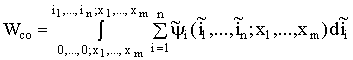 .                        (1.120)

Соотношение между энергией и коэнергией в соответствии с (1.66):

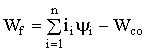 .                                     (1.121)

При подстановке (1.121) в (1.119) определяется

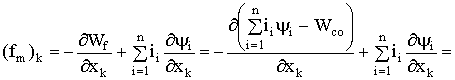
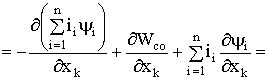
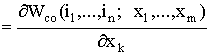  .                                 (1.122)

Электромагнитная сила по (1.122) определяется при постоянстве всех токов в течение любого виртуального перемещения.

Уравнения (1.119) и (1.122) дают силу   в случае, когда независимыми переменными являются токи   и перемещения  .

Если требуется выразить энергию через независимые потокосцепления   и перемещения  , то функционалы, определяющие связи в системе и поддерживаемые в течение всего возможного перемещения, имеют вид:

  ;                                 (1.123)

и

  .                           (1.124)

Использование в уравнении (1.108a ) определенных уравнениями (1.123) и (1.124) независимых переменных   и   дает

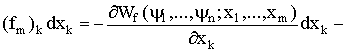
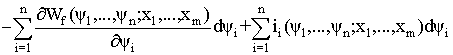 .           (1.125)

В рассматриваемом случае при установлении значений потокосцеплений энергия, запасенная в магнитном поле, подводится от электрических цепей и равна

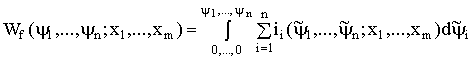 . (1.126)

Тогда два последних слагаемых в правой части (1.125) в сумме равны нулю и электромагнитная сила

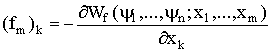 .                      (1.127)

Здесь (в (1.127)) электромагнитная сила вычисляется при постоянстве всех потоков для любого виртуального перемещения.

При независимых переменных   и   электромагнитная сила, выраженная через коэнергию

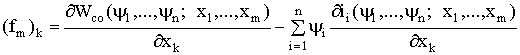 . (1.128)

Итак, получены четыре уравнения для силы   - (1.119), (1.122), (1.127) и (1.128). Они равнозначны и дают тождественно одинаковую силу. Она является действительной силой для данного положения системы, то есть для данных значений  ,   и  .