Токи в фазах (![]() ) и (
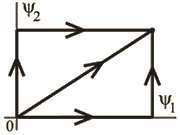
) и (![]() ) на рис.1.41 определяют эти фазы как две раздельные обмотки, возбуждающие поле, – обмотки возбуждения. При определении энергии такой системы необходимо доопределить уравнения (1.61) и (1.62) с тем, чтобы учесть дополнительное возбуждение.
) на рис.1.41 определяют эти фазы как две раздельные обмотки, возбуждающие поле, – обмотки возбуждения. При определении энергии такой системы необходимо доопределить уравнения (1.61) и (1.62) с тем, чтобы учесть дополнительное возбуждение.
Систему с двумя обмотками возбуждения определяют два семейства кривых намагничивания:
![]() ,
, ![]() . (1.95)
. (1.95)
Считаем, что ![]() - ток в обмотке (
- ток в обмотке (![]() ) и
) и ![]() - ток в обмотке (
- ток в обмотке (![]() ).
).
Запасенная энергия, как и ранее, определяется разностью потребляемой энергии и потерь энергии при изменении состояния системы от нулевых значений возбуждающих токов (потокосцеплений) до их конечных значений. Положения контуров (обмоток) при этом поддерживается неизменным (![]() ). Система в конечное состояние может быть приведена теперь множеством различных путей, поскольку вариации
). Система в конечное состояние может быть приведена теперь множеством различных путей, поскольку вариации ![]() и
и ![]() могут быть самыми различными при
могут быть самыми различными при ![]() : вначале
: вначале ![]() увеличивается от нуля до конечной величины при поддержании
увеличивается от нуля до конечной величины при поддержании ![]() постоянным и равным нулю, А затем
постоянным и равным нулю, А затем ![]() увеличивается от нуля до конечной величины при неизменном
увеличивается от нуля до конечной величины при неизменном ![]() , соответствующим его достигнутой постоянной величине:
, соответствующим его достигнутой постоянной величине:
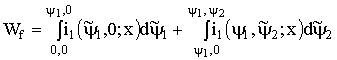 , (1.96)
, (1.96)
где ![]() и
и ![]() - конечные значения потокосцеплений обмоток.
- конечные значения потокосцеплений обмоток.
Обозначения в (1.96) определяют, что при вычислении первого интеграла ![]() и
и ![]() , а при вычислении второго
, а при вычислении второго ![]() и
и ![]() .
.
Можно изменить порядок возбуждения системы. Вначале считаем, что возбуждена обмотка (![]() ), а обмотка (
), а обмотка (![]() ) невозбуждена; затем возбуждается обмотка (
) невозбуждена; затем возбуждается обмотка (![]() ):
):
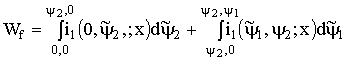 . (1.97)
. (1.97)
Можно предположить. что траектория движения системы определяется одновременным возбуждением обмоток, например так, что потокосцепления (или токи) изменяются пропорционально:![]() . Тогда
. Тогда
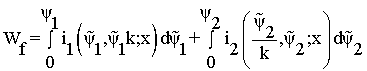 . (1.98)
. (1.98)
В рассматриваемом случае, когда система возбуждается двумя сигналами, ее энергия
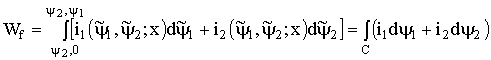 (1.99)
(1.99)
определяется интегралом, вычисляемым по контуру ![]()
![]() . (1.100)
. (1.100)
|
Такие интегралы называются криволинейными. Контур |
|
|
Конечно, необходимо убедиться в том, что заданные функционалы ![]() и
и ![]() удовлетворяют условию независимости значения
удовлетворяют условию независимости значения ![]() от пути интегрирования. Для двумерного случая (зависимости
от пути интегрирования. Для двумерного случая (зависимости ![]() от
от ![]() и
и ![]() ) необходимым и достаточным условием независимости нахождения значения интеграла для
) необходимым и достаточным условием независимости нахождения значения интеграла для ![]() от пути интегрирования является равенство:
от пути интегрирования является равенство:
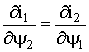 . (1.101)
. (1.101)
ЗАДАЧА
Система с двумя обмотками возбуждения определяется уравнениями связи:
![]() ;
; ![]() .
.
1. Можно ли в этой системе определить запасенную энергию как функцию состояния?
2. Найти энергию поля, когда ![]() ,
, ![]() .
.
3. Найти энергию поля, интегрируя вдоль пути ![]() для случая, когда
для случая, когда ![]() .
.
Можно представить, что в общем случае электромеханическая система (преобразователь энергии) на рис.1.11, принцип действия которой основан на явлении электромагнитной индукции, имеет ![]() пар электрических зажимов и
пар электрических зажимов и ![]() пар механических зажимов. Это определяет то, что система имеет
пар механических зажимов. Это определяет то, что система имеет ![]() степеней свободы, а уравнения связей переменных имеют вид:
степеней свободы, а уравнения связей переменных имеют вид:
![]() . (1.102)
. (1.102)
Энергетическая функция (1.99) вычисляется тогда как
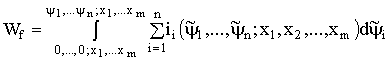 . (1.103)
. (1.103)
Следует отметить, что в уравнениях (1.102) можно вместо потокосцеплений ![]() независимыми переменными считать токи
независимыми переменными считать токи ![]() . Тогда
. Тогда
![]() . (1.104)
. (1.104)