Пусть катушка с током   расположена на поверхности гладкого цилиндрического ротора электрической машины (рис.1.38).

 
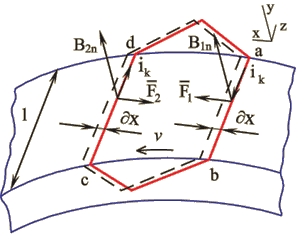
Рис.1.38

Кроме этой цепи тока могут существовать и другие, как на этой вращающейся части, так и на другой – неподвижной. Пусть всего цепей  , и в одной из этих цепей, в  -й, ток равен  . Уравнение работы, совершаемой источниками, может быть записано в виде

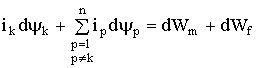  , (1.79)

где   и   - соответственно потокосцепления с рассматриваемой катушкой и с  ‑й из остальных  . Изменение потокосцеплений катушек может быть обусловлено как изменениями токов в отдельных или во всех катушках, так и изменениями положений катушек. Различая эти изменения, напишем, что

  ,        ,                    (1.80)

  и   - изменения потокосцепления  -й катушки при изменении тока ( ) и положения (координаты  ). Вообще,   и   - изменения переменных системы при изменении тока   и координаты  .

Если все катушки неподвижны, то механическая работа равна нулю, и по уравнению (1.79)

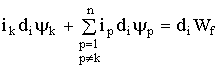  .                               (1.81)

Учитывая уравнение (1.80), из уравнений (1.79) и (1.81) получаем:

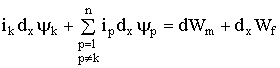  .                            (1.82)

Механическая работа по уравнению (1.82) будет найдена при определении изменения магнитной энергии, вызываемого изменением взаимного расположения катушек при постоянных токах в них.

Пусть характеристики намагничивания системы линейны. Тогда полная энергия  , запасенная в поле системы катушек, определится суммой вкладов каждой из них:

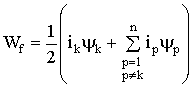                                       (1.83)
и, принимая во внимание (1.82),

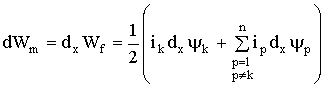  .                             (1.84)

Обозначим:   - потокосцепление  -й катушки, возбуждаемое только этой  -й катушкой;   - потокосцепление  -й катушки, возбуждаемое только другой -й катушкой с током;   - потокосцепление  -й катушки, возбуждаемое рассматриваемой  -й катушкой. Выполним очень малое перемещение  этой  -й катушки относительно других катушек (1.38), считая их неподвижными. Тогда слагаемые в правой части уравнения (1.84):

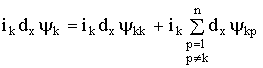  ,                                (1.85)

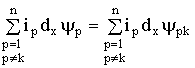  .                                    (1.86)

Для линейной системы  ,  , и  . Поэтому уравнение (1.86) можно представить в следующем виде:

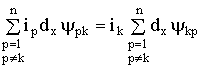  .                        (1.87)

В соответствии с уравнениями(1.84)-(1.87):

  ,                              (1.88)

где 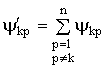  - потокосцепление  -й катушки, возбуждаемое всеми остальными   катушками. Второе слагаемое в правой части уравнения (1.88) мало, а для электрической машины, имеющей постоянный зазор  , оно равно нулю. Электромагнитная сила, действующая на катушку, в этом случае

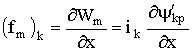  .                                    (1.89)

Далее предполагается, что катушка состоит из   витков, ее стороны имеют бесконечно малую ширину и совпадают с образующими цилиндрической поверхности, и нормальная составляющая индукции   на поверхности ротора не изменяется на его длине l (рис.1.38). Тогда, по определению потокосцепления,

  ,                                  (1.90)

где   и   - нормальные составляющие индукции, возбуждаемой всеми остальными катушками (токами) в точках окружности, через которые проходят средние линии сторон рассматриваемой  -й катушки.

Электромагнитная сила, действующая на катушку, по (1.90) и (1.89):

  .                                    (1.91)

Определенная уравнением (1.89) сила   положительна – действует в направлении перемещения  , если знак изменения потока поля, вызванного током  , совпадает со знаком изменения потока, вызванного перемещением на  .

Для быстрого определения направления силы три пальца левой руки расположим так, чтобы указательный, средний и большой пальцы образовали систему координат: указательный палец совпадает с направлением вектора индукции магнитного поля, средний – с направлением тока, большой палец указывает направление силы (рис.1.38).