Если принять, что активное сопротивление  электрического контура мало (), то из уравнения Максвелла для контура после интегрирования:

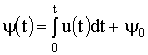  .       (1.75)

При напряжении  постоянном и равном 

 .            (1.76 )

В тех случаях, когда  равно нулю, потокосцепление  не зависит от времени, и

 .                         (1.77)

Будем считать, что устройство, представленное на рис.1.29, имеет линейные характеристики  для различных значений , , , … .Эти характеристики приведены на рис.1.37. Очевидно, что создавая положительные магнитодвижущие силы (), можно получать линейные увеличения потокосцепления  во времени до любого значения. Изменяя значения  и , можно получать необходимую зависимость .

 
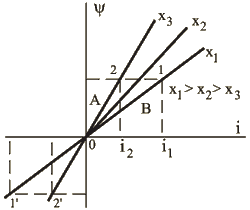
Рис.1.37

В начале координат (рис.1.37) , ,  равны нулю, а . Увеличивая магнитодвижущую силу, мы, тем самым, увеличиваем потокосцепление  до значения  в точке 1. В этой точке, при установлении , поддерживаем  по (1.77). Источник сообщил системе энергию, равную площади ; эта энергия накопилась в поле. Предоставим возможность якорю перемещаться на  ( отрицательно). Это перемещение обусловлено силой магнитного притяжения - электромагнитной силой ; координата  изменяется от значения  до значения . При этом совершается механическая работа, а траектория изменения переменных ,  и  - линия. При  электрическая энергия из сети не потребляется () и выполненная механическая работа равна по величине уменьшению энергии поля (площади ):

 .                                                    (1.78)

Приложим к зажимам обмотки возбуждения электромагнита отрицательное напряжение; потокосцепление  уменьшается до нуля по линии , а энергия, равная площади , возвращается в сеть. Площадь  меньше первоначально сообщенной энергии на величину проделанной механической работы. Если система совершает движение по траектории , то энергия передается из электрической сети магнитному полю, а от поля – подвижной части, совершающей механическую работу.

Для представления процесса преобразования энергии необходимо определить знаки изменений составляющих энергии ,  и . Условимся о следующем:

изменение электрической энергии  положительно, если электрическая цепь отдает энергию магнитному полю;

изменение энергии магнитного поля  положительно, если оно увеличивает ее запас;

изменение механической энергии   положительно, если энергия, запасенная в поле, преобразуется в механическую.

Будем изменять состояние системы, начиная движение с участка траектории  (рис.1.37). Увеличивая от нуля магнитодвижущую силу, достигаем точки . Источник напряжения сообщил системе энергию, запасаемую в магнитном поле и равную площади . Устанавливаем  и поддерживаем .

Затем подвижная часть системы (якорь) перемещается при сохранении  в новое положение (точка ) на расстояние  между  и . При этом в системе устанавливается новый ток  и система движется по линии . За счет работы внешней силы, обеспечивающей перемещение на , магнитная энергия увеличивается на величину, равную площади . И энергия, запасенная в поле, определяется площадью (). Если потокосцепление  уменьшается до нуля по пути , то в сеть уходит энергия, соответствующая площади ().

Если система движется по траектории , то энергия передается из электрической сети полю, а затем часть энергии поля – в механическую часть. В этом случае энергетические процессы определяют двигательный режим в системе.

При движении системы по пути  поступившая извне механическая энергия преобразуется в электрическую; посредником в этом преобразовании является магнитное поле. В этом случае энергетические процессы определяют генераторный режим в системе.

Для создания магнитных полей могут использоваться переменные токи (переменные МДС). В этом случае характеристики намагничивания  будут иметь продолжения в третьем квадранте (рис.1.37). И, например, двигательный режим устройства определится траекторией .