При известном изменении механической энергии электромагнитная сила определяется из уравнения

 ,                                                   (1.69)

где  - изменение координаты подвижной части устройства.

В рассмотренных случаях, когда ток  или потокосцепление , уравнения для  можно записать в удобной для расчетов форме.

Если неизменно потокосцепление (), то потребляемая электрическая энергия равна нулю, поскольку , и

 

 ,                                (1.70)

 

а электромагнитная средняя сила

 

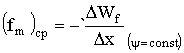 .                                                (1.71)

 

Если при возбуждении системы неизменным остается ток  (), то, в соответствии с (1.66) и (1.67),

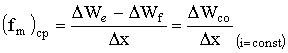 .                                    (1.72)

Уравнения (1.71) и (1.72) в пределе, когда  стремится к нулю, принимают вид:

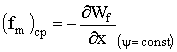 ,                                       (1.73)

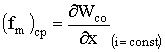  .                                         (1.74)

Пример 1-1

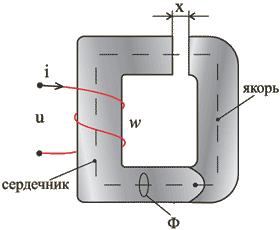
Рассмотрим электромагнит, устройство которого приведено на рис.1П. Сердечник и якорь изготовлены из ферромагнитного материала. Электромагнитная сила при бесконечно малом изменении положения якоря   по определению  .                  (1П.1)

Рис.1.П

При определении механической работы в магнитном поле по (1.54) было указано, что  - очень малая элементарная работа. При определении элементарной работы при перемещении на  возможно любое из допущений: принимать ли постоянным ток  или потокосцепление  катушки (можно ли принимать какие либо другие допущения?).

Рис.1.30 убеждает в том, что при бесконечно малом перемещении при любом из указанных допущений элементарная работа  изменяется на величину высшего порядка.

Пусть при движении на  постоянным остается потокосцепление катушки  (на рис.1П пунктиром показан поток ). Не будем учитывать потоки рассеяния устройства и их изменения при движении в системе. При этом можно учитывать только магнитную энергию в зазоре ,  поскольку при  магнитная энергия в железе также постоянна.

Примем следующие допущения:

-      полюс сердечника и находящаяся против него поверхность якоря есть равные и параллельные поверхности;

-      линии индукции поля в зазоре между полюсом сердечника и якорем перпендикулярны их поверхностям;

-      выпучиванием линий индукции поля в зазоре  пренебрегаем.

Обозначим поверхность полюсов сердечника .

Полное потокосцепление системы

 .                                                                (1П.2)

Если потокосцепление  и МДС  (ток ) пропорциональны, то магнитная энергия, запасенная в поле

 .                                                          (1П.3)

Запасенную в поле магнитную энергию можно выразить через проводимость   на пути потока по (1.43):

           () ,             (1П.4)

либо через величину, обратную магнитной проводимости, - магнитное сопротивление 

      ( ).                    (1П.5)

Сила взаимодействия ферромагнитных частей, разделенных зазором , может быть получена по (1.75) при изменяющихся  и .

Поскольку в этом случае

 ,                                                   (1П.6)

то сила

 .                                                (1П.7)

Но , и

 .                                                              (1П.8)

Можно считать, что при виртуальном перемещении изменяются поток  и магнитное сопротивление . Тогда при малых изменениях  и  в соответствие с (1П.5) можно записать:

 .                                         (1П.9)

В этом случае электромагнитная сила по (1.74):

 .                                     (1П.10)

Для устройства на рис.1П магнитное сопротивление на пути потока складывается из сопротивления стали  и сопротивления зазора . В случае, когда поле однонаправлено и равномерно распределено по сечению рассматриваемого объема,

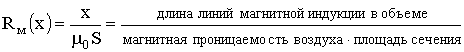 .              (1П.11)

Тогда по уравнению (1.П.10)

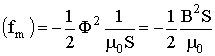 .                                        (1П.12)