|
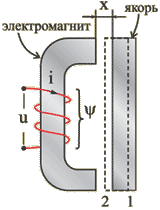
Пусть к сети с напряжением u подключен электромагнит (рис.1.29). Якорь притягивается электромагнитом и совершает механическую работу, перемещаясь из начального положения 1 в конечное положение 2 за время
|
|
|
Необходимо полагать, что ток ![]() в выражении под знаком интеграла в (1.52) зависит от потокосцепления
в выражении под знаком интеграла в (1.52) зависит от потокосцепления ![]() и координаты
и координаты ![]() (
(![]() ). Правая часть уравнения (1.52) содержит не только приращение магнитной энергии
). Правая часть уравнения (1.52) содержит не только приращение магнитной энергии ![]() за время
за время ![]() , но и механическую работу
, но и механическую работу ![]() , совершенную якорем:
, совершенную якорем:
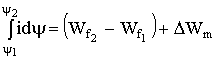 . (1.53)
. (1.53)
В дифференциальной форме
![]() . (1.54)
. (1.54)
Здесь ![]() означает не изменение механической работы, но очень малую элементарную работу.
означает не изменение механической работы, но очень малую элементарную работу.
|
При нахождении магнитной энергии |
|
|
Потребляемая системой энергия
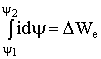 (1.55)
(1.55)
в части расходуется при перемещении якоря.
Определим ее часть, расходуемую на изменение энергии, запасенной полем ![]() . Состояния системы определяются значениями
. Состояния системы определяются значениями ![]() и
и ![]() :
:
![]() , (1.56)
, (1.56)
![]() . (1.57)
. (1.57)
Изменение энергии поля
![]() . (1.58)
. (1.58)
Уравнение баланса энергии определяет механическую энергию, обусловленную изменением состояния системы (изменения ![]() ,
, ![]() ,
, ![]() ):
):
![]() . (1.59)
. (1.59)
Если принять для рассматриваемой системы характеристику намагничивания ![]() линейной, то энергетические соотношения упрощаются.
линейной, то энергетические соотношения упрощаются.
Пусть во время ![]() движения якоря на
движения якоря на ![]() ток
ток ![]() сохраняет постоянную величину, что с достаточным приближением соответствует процессам в электромагните постоянного тока при достаточно медленном движении якоря. Изменения
сохраняет постоянную величину, что с достаточным приближением соответствует процессам в электромагните постоянного тока при достаточно медленном движении якоря. Изменения ![]() и
и ![]() при перемещении из положения 1 в положение 2 приведены на рис.1.31.
при перемещении из положения 1 в положение 2 приведены на рис.1.31.
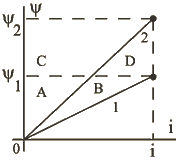
Рис.1.31
Для этого случая:
![]()
![]()
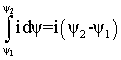
и, в соответствии с (1.53)
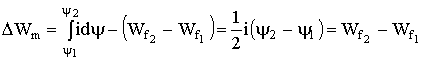 -
-
энергия ![]() , полученная из электрических сетей, за вычетом электрических потерь
, полученная из электрических сетей, за вычетом электрических потерь ![]() наполовину преобразуется в механическую работу (
наполовину преобразуется в механическую работу (![]() ); другая половина ее расходуется на увеличение магнитной энергии (
); другая половина ее расходуется на увеличение магнитной энергии (![]() ), запасенной в поле. Механическая работа равна приращению магнитной энергии.
), запасенной в поле. Механическая работа равна приращению магнитной энергии.
А теперь положим, что во время ![]() движения якоря на
движения якоря на ![]() потокосцепление
потокосцепление ![]() катушки электромагнита (рис.1.29) сохраняет постоянную величину. Изменения
катушки электромагнита (рис.1.29) сохраняет постоянную величину. Изменения ![]() и
и ![]() для этого случая приведены на рис.1.32.
для этого случая приведены на рис.1.32.
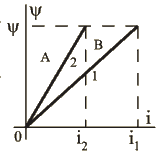
Рис.1.32
При переходе из состояния 1 в состояние 2
![]() ,
,
![]() ,
,
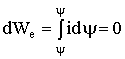 ,
,
и ![]() -
-
механическая работа равна уменьшению энергии, запасенной в магнитном поле, а электрические потери ![]() покрываются сетью.
покрываются сетью.
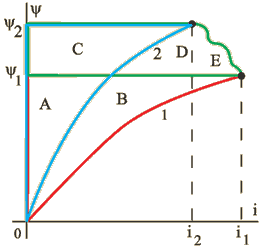
Пусть имеется произвольное изменение в системе, которое определяет изменение всех трех переменных - ![]() ,
, ![]() ,
, ![]() . Рисунок 1.33 показывает энергетические состояния в этом случае (
. Рисунок 1.33 показывает энергетические состояния в этом случае (![]() ).
).
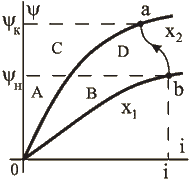
Рис.1.33
Очевидно, в соответствии с изложенным выше:
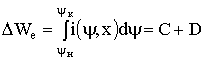 ; (1.60)
; (1.60)
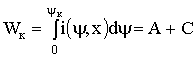 ; (1.61)
; (1.61)
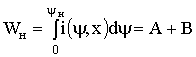 ; (1.62)
; (1.62)
![]() ; (1.63)
; (1.63)
![]() . (1.64)
. (1.64)
Как и ранее, механическая энергия равна площади между начальной ![]() и конечной
и конечной ![]() кривыми намагничивания и траекторией ab перехода.
кривыми намагничивания и траекторией ab перехода.
Необходимо отметить разницу между интегралами, выражающими энергию, поступающими из электрических сетей ![]() , и энергию, запасенную в магнитном поле
, и энергию, запасенную в магнитном поле ![]() . В интегралах для энергии поля (1.61 и 1.62) значения координат
. В интегралах для энергии поля (1.61 и 1.62) значения координат ![]() остаются неизменными. Поэтому функция
остаются неизменными. Поэтому функция ![]() является приближением (в том числе аналитическим) одной из кривых намагничивания системы (рис.1.23). Знак в виде волнистой линии
является приближением (в том числе аналитическим) одной из кривых намагничивания системы (рис.1.23). Знак в виде волнистой линии ![]() (тильда) над буквенным обозначением переменной определяет здесь и далее изменяющуюся переменную. Функция
(тильда) над буквенным обозначением переменной определяет здесь и далее изменяющуюся переменную. Функция ![]() зависит от внутренних магнитных свойств устройства. Интеграл (1.60) для энергии от электрических сетей включает функцию
зависит от внутренних магнитных свойств устройства. Интеграл (1.60) для энергии от электрических сетей включает функцию ![]() , в которой
, в которой ![]() и
и ![]() переменны. Эта функция не соответствует ни одной из кривых намагничивания; свойства ее определяются не только внутренним магнитным состоянием устройства, но и электромагнитными процессами в системе. Влияние этих процессов существенно, а учет их сложен и, поэтому, целесообразны приближенные решения задачи нахождения энергетических соотношений в электромеханической системе.
переменны. Эта функция не соответствует ни одной из кривых намагничивания; свойства ее определяются не только внутренним магнитным состоянием устройства, но и электромагнитными процессами в системе. Влияние этих процессов существенно, а учет их сложен и, поэтому, целесообразны приближенные решения задачи нахождения энергетических соотношений в электромеханической системе.
Обратимся снова к зависимости ![]() , представленной на рис.1.34. При
, представленной на рис.1.34. При ![]() механическая энергия
механическая энергия
![]() .
.
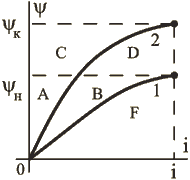
Рис.1.34
В отличие от (1.64) эту площадь можно получить как разность площадей, находящихся под конечной и начальной кривыми намагничивания. Эти площади – коэнергии (лат. со – совместно). Коэнергия для заданного тока ![]() определяется интегралом:
определяется интегралом:
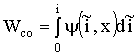 . (1.65)
. (1.65)
Между энергией поля и коэнергией существует понятное соотношение:
![]() . (1.66)
. (1.66)
Последнее уравнение определяет очевидное равенство суммы площадей, лежащих выше и ниже всякой линии, соединяющей противоположные углы прямоугольника со сторонами ![]() и
и ![]() , и площади этого прямоугольника (рис.1.35). Произведение
, и площади этого прямоугольника (рис.1.35). Произведение ![]() на
на ![]() - мера электрической энергии, поступающей в систему из сетей.
- мера электрической энергии, поступающей в систему из сетей.
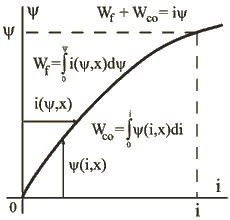
Рис.1.35
Механическую энергию в случае, когда ![]() , можно выразить через разность между начальным и конечным значением коэнергии
, можно выразить через разность между начальным и конечным значением коэнергии
![]() . (1.67)
. (1.67)
Этот результат подтверждается соотношениями, приведенными на рис.1.34.
![]() ;
;
![]() ;
;
![]() .
.
Коэнергию можно истолковывать следующим образом. Есть обмотка (рис.1.36), состоящая из двух слоев, намотанных в противоположные стороны (бифилярная намотка). Магнитодвижущие силы слоев компенсируют друг друга и зависимость ![]()
![]() является прямой
является прямой ![]() . Катушка включена в электрическую цепь, и ток
. Катушка включена в электрическую цепь, и ток ![]() всегда.
всегда.
Если стаскивать наружный слой обмотки, то потокосцепление ![]() становится отличным от нуля, и совершается механическая работа силами, обусловленными, очевидно, взаимодействием в магнитном поле, поскольку других сил нет. Если наружный слой возвращается в прежнее положение, то вновь совершается механическая работа сил в магнитном поле. При этих перемещениях от источника потребляется электрическая энергия, соответствующая площади
становится отличным от нуля, и совершается механическая работа силами, обусловленными, очевидно, взаимодействием в магнитном поле, поскольку других сил нет. Если наружный слой возвращается в прежнее положение, то вновь совершается механическая работа сил в магнитном поле. При этих перемещениях от источника потребляется электрическая энергия, соответствующая площади
![]() , (1.68)
, (1.68)
приведенной на рис.1.35.
Полагая, что система на рис.1.36. линейна, справедливо равенство ![]() и
и ![]() . Энергия поля
. Энергия поля ![]() может быть возвращена в электрические сети, если ток в катушке уменьшается до нуля (система отключается от источника). Второе слагаемое
может быть возвращена в электрические сети, если ток в катушке уменьшается до нуля (система отключается от источника). Второе слагаемое ![]() (коэнергия) в левой части (1.68) соответствует механической энергии, проявляющейся при снятии слоя катушки или возвращении его. При работе электромагнитного устройства коэнергия не запасается; имеет смысл лишь изменение ее
(коэнергия) в левой части (1.68) соответствует механической энергии, проявляющейся при снятии слоя катушки или возвращении его. При работе электромагнитного устройства коэнергия не запасается; имеет смысл лишь изменение ее ![]() .
.
Рис.1.36
Динамика изменения механической силы в магнитном поле представлена динамической моделью:
Представим, что решена задача, связанная с нахождением либо величины энергии в системе, либо изменением ее.
Пусть электромагнитная система определена характеристиками, приведенными на рис.1.23. В этом случае энергия рассчитывается при нахождении интегралов (1.61) и (1.62)
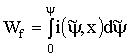 .
.
Решение его дает зависимость энергии ![]() от
от ![]() и
и ![]() ; эти
; эти ![]() и
и ![]() соответствуют единственной точке на единственной из кривых намагничивания и определяется единственным значением тока
соответствуют единственной точке на единственной из кривых намагничивания и определяется единственным значением тока ![]()
Принимаем, что каждая такая единственная точка определяет одно возможное энергетическое состояние системы. Тогда каждому такому состоянию соответствует одно и только одно количество энергии, запасенное в магнитном поле. В этом случае говорят об энергии в системе (энергии поля) как функции состояния системы или – силовой функции. Функция состояния не зависит от пути (траектории процесса), следуя которому система пришла в рассматриваемое равновесное состояние – и поэтому функция состояния не зависит от предыстории системы. Функция состояния определяет свойства системы в зависимости от конечных значений переменных (![]() ) – их значений в рассматриваемой точке. Тогда значения интегралов вида (1.61) и (1.62) не зависят от пути интегрирования. Это означает, что значение функции, определяющей энергию системы, будет одним и тем же, если рассматриваемое состояние системы достигнуто на различных траекториях. То, что энергия
) – их значений в рассматриваемой точке. Тогда значения интегралов вида (1.61) и (1.62) не зависят от пути интегрирования. Это означает, что значение функции, определяющей энергию системы, будет одним и тем же, если рассматриваемое состояние системы достигнуто на различных траекториях. То, что энергия ![]() есть функция состояния, позволяет установить значения переменных в системе независимо от переходного процесса, определяющего конфигурацию системы (расположение элементов ее - координаты
есть функция состояния, позволяет установить значения переменных в системе независимо от переходного процесса, определяющего конфигурацию системы (расположение элементов ее - координаты ![]() ) и величину возбуждающего воздействия (
) и величину возбуждающего воздействия (![]() или
или ![]() ).
).
При этом можно вначале, не возбуждая систему, составить ее механически, установив требуемые значения координат ![]() . А затем, не изменяя
. А затем, не изменяя ![]() , возбуждать систему, увеличивая токи
, возбуждать систему, увеличивая токи ![]() или потокосцепления
или потокосцепления ![]() от начальных нулевых до конечных значений.
от начальных нулевых до конечных значений.
Можно вначале возбудить систему, а затем составить ее механически.
В обоих случаях конечное значение запасенной энергии поля одинаково.
Понятие функции состояния определено только для систем без рассеяния энергии. При необходимости рассеяние учитывается отдельно.
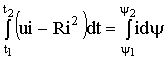 . (1.52)
. (1.52)