Представим электрическую цепь с источником напряжения . Элементы цепи не могут совершать перемещений, вызывающих изменения конфигурации цепи и ее положения в пространстве. Для определения состояния этой цепи можно использовать уравнение Максвелла для контура (1.28):

.

Умножим левую и правую части этого уравнения на  и проинтегрируем от , когда  и , до , когда потокосцепление достигает определенного (известного) значения :

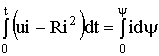  .                                          (1.51a )

В уравнении (1.51)  - электрическая энергия, поступающая в цепь из сети, 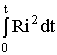 - потери энергии в активном сопротивлении цепи. Разность этих энергий расходуется на создание магнитного поля, поскольку электрическая цепь неподвижна и, следовательно, в процессе нарастания тока  и потокосцепления  за время  не совершается механической работы и нет других проявлений энергетического процесса.

Энергия, запасенная в поле и равная

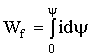 ,                                               (1.51b )

называется магнитной энергией.