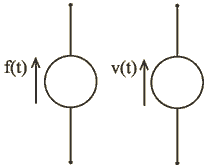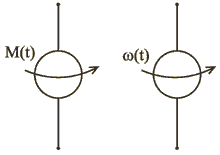Поскольку система представлена сосредоточенными параметрами, то решению будут подлежать задачи теории цепей, а уравнения движения – обыкновенные дифференциальные уравнения.
Рассматриваются движения твердых тел. Такие тела совершают либо поступательное, либо вращательное, либо поступательно-вращательное движение. В последнем случае поступательное и вращательное движения динамически независимы друг от друга, если мгновенные вращения проходят через центр тяжести тела; движение произвольной точки тела задается шестью координатами: тремя координатами x , y , z , характеризующими перемещение его центра тяжести, и тремя координатами φ , ψ , θ , характеризующими вращение тела вокруг трех взаимно перпендикулярных осей, проходящих через центр тяжести.
Механические системы классифицируются в зависимости от числа координат, необходимых для описания движений, совершаемых их материальными точками. Например, вращающийся вокруг своей оси ротор электрической машины является однокоординатной системой или системой с одной степенью механической свободы. В этом случае единственная координата – угол поворота ротора φ . Координаты системы, их производные или их интегралы, определяющие характеристики движения системы, входят в уравнения движения в качестве независимых переменных.
|
Методы анализа электрических цепей переносятся на механические цепи. Как и электрические цепи, механические цепи состоят из активных и пассивных элементов. Активные элементы являются источниками энергии. Если система движется поступательно, то в такой системе могут быть источники двух видов: источники силы иисточники скорости. Источник силы в механической цепи – приложенная к системе заданная внешняя сила f (t ). Если вместо силы задается скорость какой-либо точки системы v (t ), то эта известная скорость является в схеме механической цепи источником скорости, присоединенным к соответствующей точке. Источники при поступательном движении изображаются на схемах механических цепей так, как показано на рис.1.15. Стрелки указывают направление действия силы или направление действия скорости, когда функция f (t ) или v (t ) положительны. |
|
|
Масса m характеризует элемент механической цепи, обладающей инерцией. Это пассивный элемент, накапливающий кинетическую энергию поступательного движения. Считаем массу постоянной во времени и не зависящей от движения элемента. При перемещении m относительно координат на 
со скоростью 
сила, действующая на этот элемент
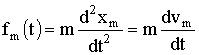. (1.33)
Величина, численно равная, но противоположная по знаку произведению массы на ускорение 
, называется силой инерции.
При интегрировании уравнения (1.33) получается выражение для скорости:
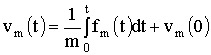. (1.34)
Пружины создают силы, стремящиеся восстановить относительные координаты системы. Это – силы, противодействующие деформации пружины. Силы, развиваемые растянутой или сжатой пружиной при данной деформации, пропорциональны ее жесткости К. Пружина – пассивный элемент, который накапливает потенциальную энергию. Сила 
, необходимая для относительного перемещения концов пружины на 
. (1.35)
Продифференцировав уравнение (1.35), получим:
. (1.36)
Демпфирующая сила, действующая в механической системе, пропорциональна относительно скорости. К таким силам относятся силы, создаваемые вязким трением, или силы электромагнитной природы, действующие на проводящие контуры, движущиеся в магнитных полях. Действия демпфирующих сил сопровождается необратимым преобразованием кинетической энергии в тепло.
В механической цепи пассивным элементом, представляющим рассеяние энергии, является элемент 
- сопротивление движению. Сила 
, необходимая для создания разности скоростей 
. (1.37)
Из (1.37) разность скоростей
. (1.38)
Условные обозначения в схемах цепей элементов m , K , приведены на рис.1.16.
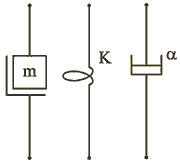
Рис.1.16
Во вращающихся системах также определяются источники энергии: источники момента и источники угловой скорости.
|
Источники энергии вращательного движения изображаются символами, приводимыми на рис.1.17. Стрелки указывают направления вращающего момента или угловой скорости, когда M (t ) и |
|
|
положительны. На вращение тела влияет не только масса тела, но и ее распределение относительно оси вращения. Инерционный элемент в этом случае – полярный момент инерции J = mr 2, где r – радиус инерции тела относительно оси вращения. Это - пассивный элемент, накапливающий кинетическую энергию.
Величина вращающего момента, сообщающего элементу 
угловое ускорение 
,
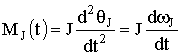. (1.39)
Упругие тела, совершающие вращательное движения и подвергающиеся скручиванию, оказывают ему сопротивление. Величина этого сопротивления пропорциональна их крутильной жесткости 
. Момент, необходимый для создания относительно углового перемещения q К(t ) концов упругого тела с крутильной жесткостью
. (1.40)
Во вращающихся системах демпфирующий момент пропорционален относительной угловой скорости. Коэффициент пропорциональности a - крутильное сопротивление илисопротивление вращению. Момент Мa (t ), необходимый для создания разности угловых скоростей w a (t )
. (1.41)
Угловые перемещения при вращательном движении могут отсчитываться по отношению к неподвижной системе координатных осей, когда взаимно уравновешены все моменты, приложенные к телу; координатная система может быть и равномерно вращающейся.
В качестве примера, поясняющего структуру механических цепей и их математическое представление, рассмотрим следующее устройство.
На рис.1.18 представлен свободный вал с двумя роторами (1 и 2). Моменты инерции роторов 
и 
соответственно. Вращающий момент 
привел систему в состояние крутильных колебаний. Составляющая 
- постоянный момент, 
- переменная часть вращающего момента. Постоянная составляющая момента уравновешивается постоянным моментом нагрузки и постоянными моментами трения. Сумма этих моментов в точности равна по величине , направлена в противоположную сторону (относительно ) и считается приложенной к ротору 2. Крутильная жесткость части вала между роторами равна . Изменения угловой скорости каждого из роторов относительно постоянной средней скорости демпфируются вязким трением, моменты которого 
и 
соответственно. Начальные скорости и угловые координаты роторов определяются составляющей момента . И если рассчитываются колебания скорости, обусловленные только переменной составляющей момента , то уравнение момента может быть записано в системе координат, вращающейся равномерно.
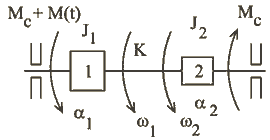
Рис.1.18
Положительное направление противоположно направлению часовой стрелки, если наблюдать его с правого конца вала. Значения 
и 
- отклонения угловых скоростей роторов от постоянной составляющей угловой скорости системы 
. Положительное их направление совпадает с положительным направлением . Схема механической цепи устройства приведена на рис.1.19.
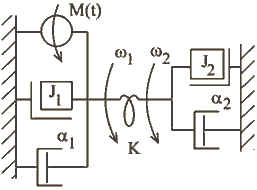
Рис.1.19
Выделенные составляющие электромеханической системы – электрическая, магнитная и механическая – могут быть рассмотрены на основе единой концепции – теории цепей. Это полагает использование единой развитой теоретической основы для анализа процессов в электромеханических преобразователях энергии. Поскольку электромеханический преобразователь энергии проявляется в единстве этих систем, то необходимо указать связи между ними.