Уравнение Максвелла
(1.21)
является дифференциальной формой закона электромагнитной индукции. Умножим левую и правую части (1.21) на 
и проинтегрируем по поверхности S , опирающейся на замкнутый контур 
:
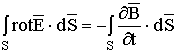. (1.22)
Применение к левой части (1.22) теоремы Стокса определяет уравнение:
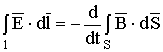. (1.23)
Здесь необходимо отметить, что явление электромагнитной индукции необязательно связано с наличием замкнутого проводника. Изменение магнитной индукции всегда сопровождается возникновением электрического поля независимо от того, есть проводник, или нет. Замкнутый проводник лишь проявляет ток при действии электрического поля. Поэтому уравнение (1.23) справедливо для любого замкнутого контура, в том числе мысленно проводимого в пространстве.
В (1.23) 
в соответствии с (1.2) и
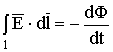. (1.24)
Уравнение (1.24) определяет электродвижущую силу индукции 
.
|
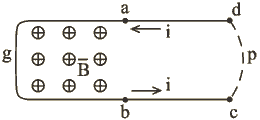
Рассмотрим контур, сцепленный в своей части с изменяющимся магнитным полем (рис.1.10). Мера магнитного поля – вектор |
|
|
. Назовем часть контура 
– внешней. Во внешней части на участке 
В рассматриваемом контуре в части 
, сцепленной с потоком 
вектора индукции 
, наводится электродвижущая сила 
, которая порождает в контуре ток 
. Необходимо определить значение интеграла в левой части (1.24). Этот интеграл равен работе сил электрического поля при перемещении единичного положительного заряда вдоль контура .
Величину 
можно представить как сумму интегралов (электродвижущих сил) на отдельных участках контура:
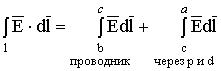. (1.25)
Проводник на участке 
обладает электрическим сопротивлением. Если внутри проводника существует электрическое поле, то это поле приводит в движение электрические заряды и появляется ток проводника. Этот ток (его мерой может быть плотность тока 
, где 
- площадь элементарного сечения проводника) пропорционален интегралу электрического поля от одного конца проводника до другого. Это определяет закон Ома в дифференциальной форме 
, где
- электрическая проводимость.
Таким образом, некоторый коэффициент пропорциональности (обозначим его 
) устанавливает связь между током и разностью потенциалов между точками b и c . Величина – электрическое сопротивление участка цепи bc , и
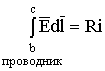. (1.26)
Интеграл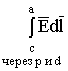 
определяется на двух участках контура. На части d -a полагается идеальный проводник. Внутри его электрических полей нет, поэтому потенциал от d до а равен нулю. И весь вклад в 
приходится на участок пути интегрирования от с до d . Считаем, что в этой части пространства нет магнитных полей и, поэтому интеграл не зависит от выбора пути. Следовательно, можно определить потенциалы точек с и d . Разность потенциалов – напряжение 
между с и d :
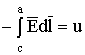. (1.27)
Уравнение (1.25) принимает вид:
, или
. (1.28)
Уравнение (1.28) называют уравнением Максвелла для контура.