Поток вектора магнитной индукции через поверхность , ограниченную каким-либо контуром, равен поверхностному интегралу вектора магнитной индукции по поверхности :

.                               (1.13)

Это уравнение справедливо для любой поверхности; контур , ограничивающий поверхность, может быть как угодно сложным. Рассмотрим контур, состоящий из трех последовательных витков на рис.1.8. В контуре ток . В рассматриваемом случае магнитное поле нельзя представить в виде потока , сцепленного с каждым из витков. На рис.1.8. видно, что поток, пронизывающий крайние витки, меньше потока, пронизывающего средний виток. Чтобы найти электродвижущую силу во всей катушке, нужно просуммировать электродвижущие силы, наводимые во всех витках.

 
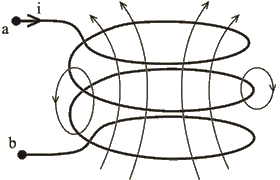
Рис.1.8

При этом вводится понятие магнитного потокосцепления:

,                                                  (1.14)

где  – поток, сцепленный с k -м витком, а сумма берется по всем виткам. Следует иметь в виду, что сложение в (1.14) следует проводить алгебраически, и положительными считаются линии магнитной индукции (и соответствующие потоки), направления которых связаны с положительным направлением тока в контуре электрической цепи правилом правого винта.

Если поток уменьшается до нуля, то каждая линия магнитной индукции столько раз пересечет контур тока, сколько раз она с ним сцеплена. Это определяет, что

.                                                   (1.15)

В ряде случаев приближенно можно считать, что все линии магнитной индукции сцепляются со всеми  витками катушки. Тогда потокосцепление .