Векторные поля обладают  важным математическими свойствами. Эти свойства будут использоваться при описании законов электромагнетизма.

Представим себе часть пространства, ограниченного замкнутой поверхностью. Определим, истекает ли "что-то" из этой поверхности?

Если рассматривается, например, поле скоростей в жидкости, то естественен вопрос: как соотносится количество жидкости, втекающее и вытекающее через поверхность в единицу времени? Количество жидкости, вытекающее через поверхность, определим "потоком скорости" через поверхность за единицу времени. Поток через элемент поверхности равен составляющей скорости, нормальной к элементу поверхности, умноженной на его площадь (рис.1.3.). А весь поток вектора ("чего-то") через произвольную поверхность получается суммированием вкладов от всех элементов поверхности  .

 
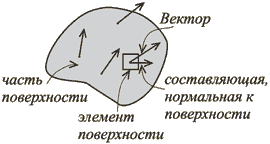
Рис.1.3

Поток вектора магнитной индукции  сквозь некоторую поверхность   называют магнитным потоком  (фи) сквозь эту поверхность. Это определение записывается в виде:

 .          (1.2)

Определение уравнения (1.2) иллюстрируется на рис.1.4.

 
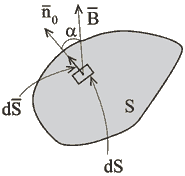
Рис.1.4

Если поверхность нормальна к вектору  , то ,  ,  . Это определяет то, что магнитная индукция является плотностью магнитного потока в данной точке поля.

Пусть поверхность   мала настолько, что в ее пределах магнитное поле можно считать однородным, тогда

                                     (1.3)

и, учитывая, (1.1),

  -                                              (1.4)

электрический заряд, переносимый в опытах 1.1.1 через поперечное сечение провода измерительной рамки, равен отношению магнитного потока   через поверхность , охватываемую рамкой в ее начальном положении, к сопротивлению R всей замкнутой цепи рамки. Магнитный поток по отношению к контуру считается положительным ( >0), если при быстром уменьшении потока до нуля положительный заряд переносится в положительном направлении контура (q >0). Если в представленных опытах рамку не выносить за пределы поля, а только перемещать ее из одного положения в поле в другое, то при каждом таком перемещении наблюдаем бросок измерительной системы гальванометра. Это свидетельствует о переносе заряда  , определяемом изменением   потока через поверхность, ограниченную рамкой.

Если поток   в начальном положении измерительной рамки был положителен, то, очевидно, при уменьшении его до нуля его приращение будет отрицательным (  ). Поскольку  >0 ( <0) при q >0, то определяется уравнение:

 ,                                                 (1.5)

которое является одной из формулировок закона электромагнитной индукции.