Для количественного представления магнитного поля можно выбрать его проявление электромагнитной индукцией, заключающееся в индуктировании электродвижущих сил в проводниках, движущихся в магнитном поле, или в неподвижных проводниках, находящихся в переменном магнитном поле.

Пусть имеется некоторое пространство вблизи одного из полюсов постоянного магнита (рис.1.1). В этом пространстве поместим плоскую рамку Р из тонкого провода. Площадь рамки – S . Тщательно свитые концы (чтобы не образовывались дополнительные контуры) рамки подключены к гальванометру Г, значительно удаленному от магнита. Гальванометр позволяет измерить заряд q , текущий в цепи, подключенной к его зажимам. Быстро отнесем рамку на значительное расстояние от ее начального положения. Отброс гальванометра (и величина q ) при таком отнесении зависит только от начального положения рамки. Если повторять опыт при постоянном начальном положении рамки, но различном сопротивлении R проводов рамки и соединительных, то выясняется, что значение q обратно пропорционально R .

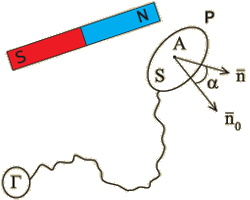Рис.1.1

Определим центр плоской поверхности S в границах рамки точкой А. Выберем положительное направление обхода ( ) по периметру рамки, находясь на внешней стороне ее поверхности S . Величина, q считается положительной, когда положительный заряд переносится в положительном направлении обхода рамки. Положительное направление нормали   приведено на рис.1.2.

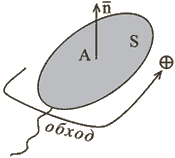Рис.1.2

Пусть, далее, центр плоской поверхности S , ограниченной рамкой, всегда совпадает с точкой А, занимающей одно и то же  положение относительно магнита. Перемещая на значительное расстояние от магнита из этой неизменной точки пространства рамку с уменьшающейся поверхностью S , убеждаемся, что q пропорционален величине S . Может быть определено направление   положительной нормали, которое соответствует наибольшему значению q при заданном значении S . При другом направлении положительной нормали  , значение q пропорционально  (  - угол между   и  ).

Проведенные наблюдения могут быть представлены зависимостью:

.                                                    (1.1)

В (1.1.) величина   есть "что-то", не зависящее от условий опыта (R ,  ,  ), но зависящее только от положения точки А по отношению к магниту. Если пробная рамка и гальванометр фиксируют "что-то", то это "что-то" остается в точке А и тогда, когда из этой точки убрали пробную (измерительную) рамку. Величина   определяет состояние среды, определенное присутствием магнита. В разных точках пространства (изменение расположения точки А), окружающего магнит, наблюдаются различные значения величины  . Эти различающиеся от точки к точке значения   есть поле. Величину   называют магнитной индукцией. Магнитная индукция – векторная величина; магнитное поле – векторное поле. Направление вектора   совпадает с определенным выше направлением  .